Definiční obor funkce je soubor všech možných hodnot, které lze dosadit za proměnnou x do dané funkce f(x) tak, že výsledek bude mít validní matematický význam a funkce bude dávat smysl. Nejjednoduším vysvětlením a pochopením problematiky definičního oboru je zhlédnout a vyřešit několik ukázkových příkladů, na kterých je možné tomu porozumět.
1. Ukázkový příklad:
![]()
Otázka zní: které hodnoty nemohu dosadit za x? Pokud se podívám na čitatel, tak vidím, že čitatel nehraje žádnou roli, protože ať dosadím za x jakoukoliv hodnotu, tak výraz bude dávat smysl, to bohužel není stejný případ u jmenovatele, protože nemohu dělit nulou, to znamená, že musím nalézt nulový bod, tedy x se nesmí rovnat jedné minus jedné polovině.
![]()
2. Ukázkový příklad:
Ne vždy musí být nalezení definičního oboru zcela jednoduché a může se od nás očekávat znalost logaritmických, goniometrických a dalších funkcí.
![]()
Výraz pod odmocninou nesmí být záporný, tedy:
![]()
Potřebujeme osamostatnit x, takže je nutné se zbavit přirozeného logaritmu, inverzní funkcí k přirozenému logaritmu je exponenciální funkce s bází e, což je Eulerovo číslo.
![]()
![]()
Jakékoliv číslo na nultou je rovno jedné.
![]()
Převedeme číslo -24 na druhou stranu rovnice.
![]()
Odmocněním obou stran rovnice získáme:
![]()
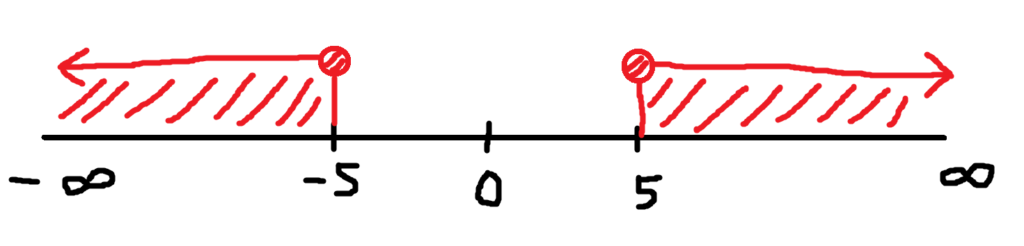
![]()
3. Ukázkový příklad:
![]()
Jmenoval se nesmí rovnat nule.
![]()
Přesuneme -1 na druhou stranu.
![]()
Kdy se sin(x) rovná 1? Vyčteme ze znalosti grafu sinus.
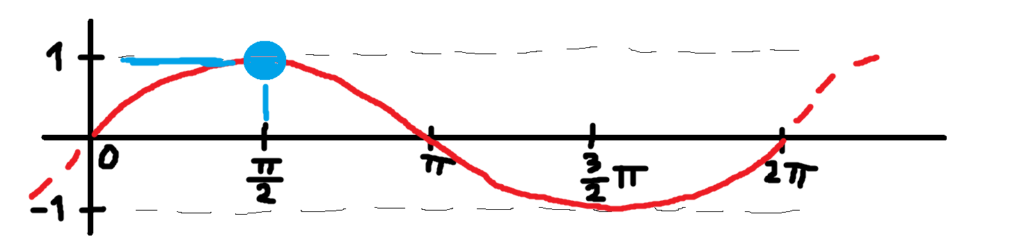
Zároveň víme, že sinus je periodická funkce a opakuje se, z toho vyplývá, že definiční obor je:
![]()