Sériové zapojení
Při sériovém zapojení rezistorů vypočítáme celkový odpor jako součet odporů všech rezistorů v daném obvodě, které jsou zapojeny sériově. Pokud budeme mít 3 rezistory o velikosti: 100, 200 a 300 ohmů, pak při sériovém zapojení jejich celkový odpor bude 600 ohmů.
![]()
Řešený příklad
Jaký bude výsledný odpor 5 stejných rezistorů, které mají odpor 200 ohmů a jsou zapojené sériově?
![]()
![]()
![]()
Paralelní zapojení
Při paralelním zapojení můžeme výsledný odpor vypočítat při dvou rezistorech jako součin rezistorů, který vydělíme součtem těchto rezistorů. Případně u dvou a více rezistorů získáme celkový odpor jako součet převrácených hodnot.
![]()
![]()
Řešený příklad
Jaký bude výsledný odpor třech rezistorů zapojených paralelně jestliže jejich odpory jsou 3, 6 a 2 ohmy?
- Způsob řešení
Při použití prvního vzorce pro vypočítání odporu můžeme vždy sčítat maximálně dva zároveň, takže musíme příklad rozdělit na dva samostatné výpočty. Pokud bychom měli 4 odpory, tak budeme muset mít 3 výpočty. Tato metoda je jednoduchá, ale je vhodná pouze pro sčítání malého množství odporů.
![]()
![]()
2. Způsob řešení
Tento vzorec se používá při počítání vícero odporů, kdy najdeme společného jmenovatele a jednoduše vypočítáme. Výsledný odpor získáme převrácením vypočítané hodnoty viz. příklad níže.
![]()
![]()
![]()
![]()
![]()
Složitý příklad
Vypočtěte výsledky odpor všech rezistorů podle zadání na obrázku, jestliže: R1 = 150 ohmů, R2 = 9 ohmů, R3 = 18 ohmů, R4 = 200 ohmů, R5 = 250 ohmů, R6 = 1000 ohmů, R7 = 256 ohmů, R8 = 72 ohmů.
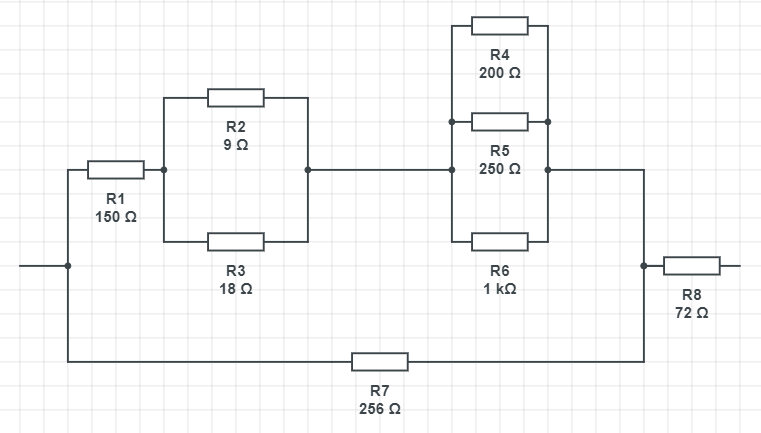
Řešení
- Nemůžeme počítat sériově a paralelně zapojené odpory dohromady (např. R1 + R2), nejdříve proto vyřešíme paralelně zapojené rezistory.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Po zjednodušení nyní vypadá naše schéma takto:
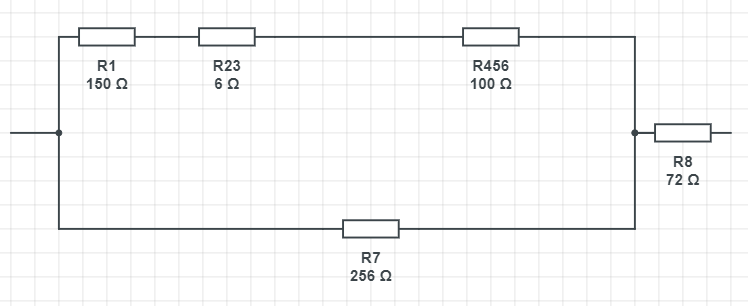
V dalším kroku sečteme sériově zapojené rezistory tedy R1, R23 a R456.
![]()
![]()
![]()
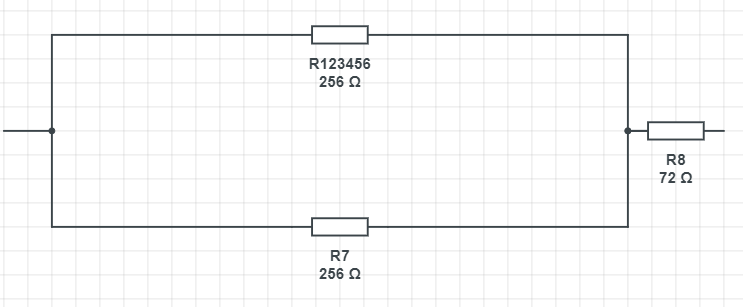
Nyní už jen zbývá vypočítat dva paralelní rezistory a následně k nim přičíst R8.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Celkový odpor všech rezistorů je 200 ohmů.