Kondenzátor je elektrotechnická součástka, která má schopnost uchovávat elektrický náboj. Kondenzátory můžeme jako rezistory spojovat a zjednodušovat jejich zapojení, obdobně jako u sériově a paralelně zapojených rezistorech. Zjednodušeně řešeno, paralelně zapojené kondenzátory se vypočítávají stejně jako sériově zapojené rezistory a sériově zapojené kondenzátory se vypočítávají stejně jako paralelně zapojené rezistory.
Paralelní zapojení
V paralelním zapojení jsou veškeré kladné póly spojeny dohromady a všechny záporné póly jsou rovněž spojeny dohromady. To znamená, že všechny kondenzátory mají stejné napětí, ale celková kapacita obvodu je součtem kapacit jednotlivých kondenzátorů. Tedy platí:
![]()
Řešený příklad
Jaká bude výsledná kapacita 3 kondenzátorů, které jsou zapojeny paralelně a jejich velikosti jsou 4, 6 a 10 mikrofaradů?
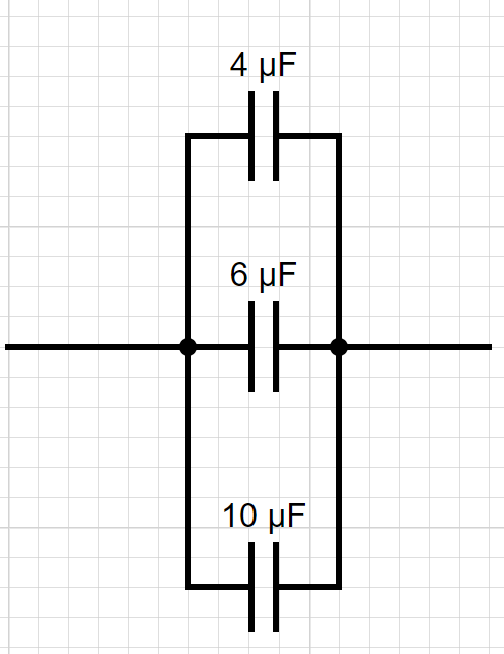
![]()
![]()
![]()
Sériové zapojení
Pokud máme dva sériově zapojené kondenzátory lze celkovou kapacitu vypočítat jako součin dvou kondenzátorů, kterou vydělíme součtem těchto kapacit. Tuto metodu lze použít i pro více kondenzátorů, ovšem musíme postupovat vždy po dvou kondenzátorech, to znamená, že pokud máme 3 sériově zapojené kondenzátory, tak tuto metodu lze použít pokud nejdříve sečteme dva kondenzátory a následně provedeme totožný postup se součtem prvních dvou kondenzátorů s třetím, případně lze použít postup, kdy pracujeme s obrácenými hodnotami.
![]()
![]()
Řešený příklad
Jaká bude výsledná kapacita všech kondenzátorů zobrazených na schématu níže po spojení do jednoho jediného?
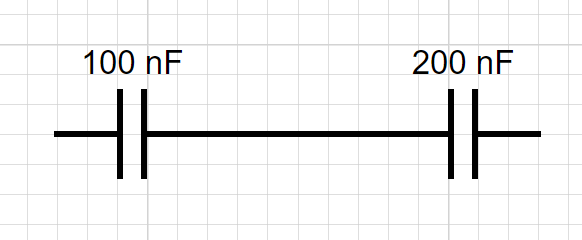
Jedná se o sériové zapojení dvou kondenzátorů, to znamená, že můžeme použít vzorec:
![]()
![]()
![]()
Složitý příklad
Kolik faradů má celková kapacita všech kondenzátorů na schématu níže, jestli platí, že C1= 1 µF, C2= 100 nF, C3= 2 µF, C4= 100 nF, C5= 100 nF, C6= 200 nF, C7= 2 µF a C8= 50 nF. Veškeré mezivýpočty i finální výpočet zaokrouhlujte na čtyři platné číslice.

Řešení
- Jelikož otázka zní kolik faradů má celková kapacita a my máme zadány různé jednotky, tak začneme tím, že si veškeré kapacity kondenzátorů přepočteme na farady.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. Vypočítáme celkovou kapacitu kondenzátorů, které jsou zapojeny za sebou, tedy sériově, konkrétně kondenzátory C2, C3, C4 a poté kondenzátory C5, C6 a C7.
Pro výpočet prvních tří kondenzátorů zvolím metodu pomocí vzorce.
![]()
Jelikož mám, ale kondenzátory tři a nikoliv dva, tak tuto metodu budu muset nejdříve použít pro první dva a následně pro součet prvního s druhým a se zbylým třetím kondenzátorem, tedy:
![]()
![]()
![]()
Nyní použijeme totožný vzorec se zbylým třetím kondenzátorem:
![]()
![]()
![]()
Ještě zjednodušíme kondenzátory C5, C6 a C7 do jednoho, ale pro procvičení vzorců využijeme vzorec:
![]()
![]()
![]()
![]()
![]()
Nyní náš již částečně zjednodušený obvod vypadá takto:
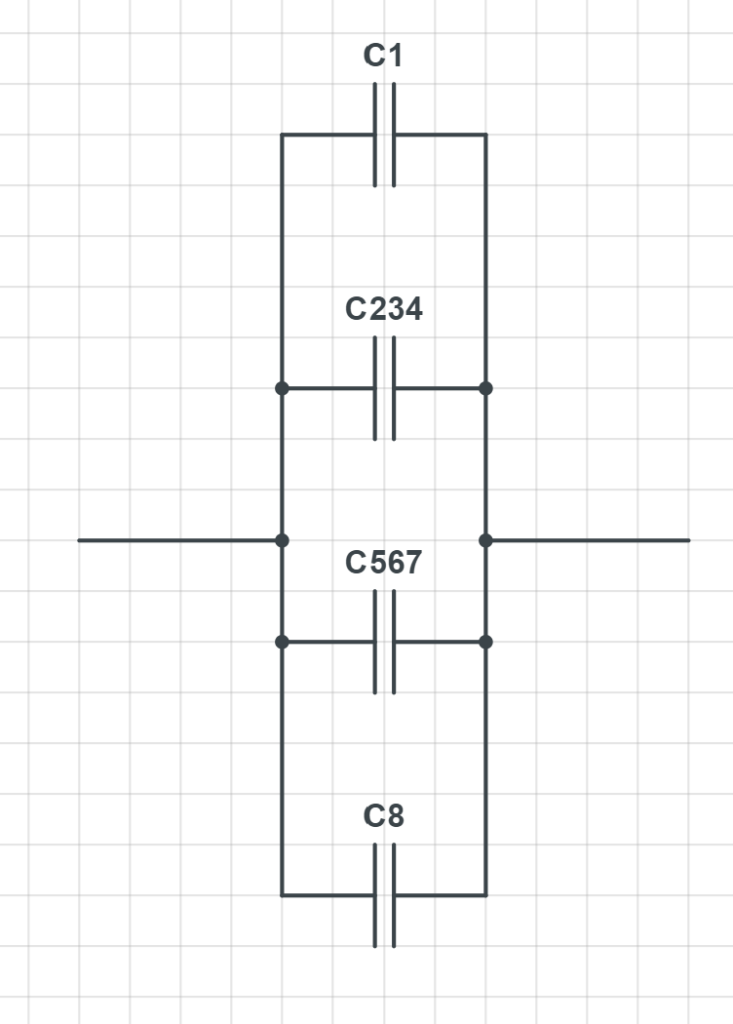
3. Nyní stačí sečíst paralelně zapojené kondenzátory a máme celkovou kapacitu.
![]()
![]()
![]()